Inverse Relationship Between Addition and Subtraction

A number fact is made up of three numbers. These three numbers can be used to make up other number facts. Knowing one fact can help children with other facts. Look at the number facts we can make with the numbers 3, 4, and 7.

Addition Facts Subtraction Facts Addition and subtraction are inverse operations because one operation can "undo" the other operation. Adding 3 and 5 to get 8 is the opposite of 8 minus 5, leaving 3.

3 + 5 = 8 and 8 – 5 = 3

addends sum difference

3 + 4 = 7 7 – 3 = 4

4 + 3 = 7 7 – 4 = 3

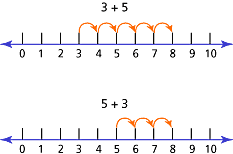
You can strengthen addition skills by investigating two special properties. Students may be familiar with the Order Property. It is also called theCommutative Property of Addition because it allows the order of the addends to be changed without affecting the sum. So, 3 + 5 has the same sum as 5 + 3.

Generally, subtraction facts are harder for children to learn than addition facts. If a child knows that 6 + 9 = 15, and he or she sees the subtraction sentence 15 – 9 = __, the child can think, 9 and what are 15? This use of thinking of the related addition fact when children encounter a subtraction fact they don't know should be encouraged. Children often find themselves either counting up or counting back to solve subtraction, and that is inefficient. If children learn the important inverse relationship between addition and subtraction, subtraction facts will become much easier. As you work with the children, use questions that encourage this strategy of the inverse relationship between addition and subtraction.

Begin your instruction by reviewing with children the related addition facts. Write 2 + 3 = 5 and 3 + 2 = 5 on the chalkboard. Ask children what they can tell you about these two addition facts. Elicit that the addends are 2 and 3 in both facts, but they are reversed. Also, the two facts have the same three numbers.

Then tell children that they are going to learn something new called a fact family. Explain that it is not a real family, but that the facts are related like people are related, therefore they have been given the name family. Point to the two addition facts that you wrote on the board and say, "Now I am going to write two related facts." Write 5 – 2 = 3 and 5 – 3 = 2 on the chalkboard. Ask, "Do you see anything the same about these two facts and the two addition facts?" Elicit that they use the same numbers. "Do you see anything different about these two facts and the two addition facts?" Children should respond that the new facts are subtraction facts and the largest number comes first in both facts. Tell children that these four facts make up a fact family.

Take time to discuss other fact families with children. Then write 3 + 3 = 6 on the chalkboard. Ask if it has another addition fact. Elicit that it does not because 3 + 3 turned around would be 3 + 3. Ask if any child can tell you what the related subtraction fact might be. (6 – 3 = 3) Discuss other doubles and why there is only one addition and one subtraction fact in fact families that have doubles.

Ask children why they think that it is important to learn fact families. Elicit that once they know one fact, that fact can help them find out the rest of the facts in the family. Tell children that they are now going to learn a lot more fact families.