Im Jahre 1908 fanden Hardy und Weinberg unabhängig voneinander ein Gesetz, das die Verteilung von Erbmerkmalen in Populationen beschreibt.

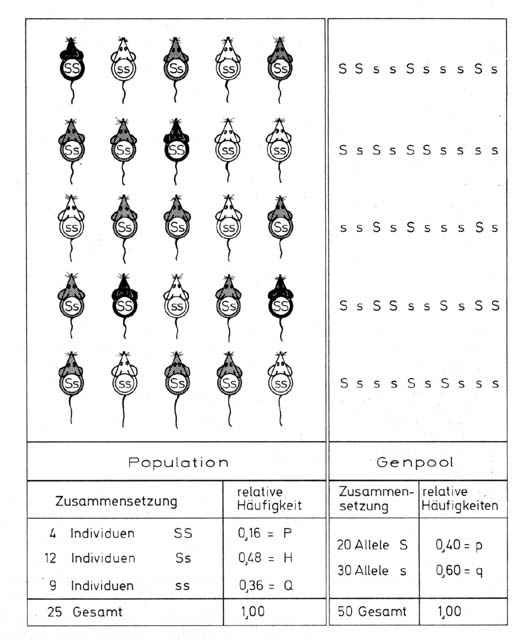
Betrachten wir eine Population mit Zufallspaarung, in der schwarze, graue und weiße Individuen (z.b. Mäuse) nebeneinander vorkommen. Die Eigenschaften schwarz und weiß werden von den Allelen eines Gens bestimmt. SS bedingt schwarze Färbung, ss weiße; die Heterozygoten Ss wären aber grau. Wenn wir den Genpool der Population betrachten, so finden wir, dass die beiden Allele S und s in der Population eine unterschiedliche Häufigkeit haben. Bezeichnen wir die relative Häufigkeit von S mit p und die von s mit q, so können wir, wenn wir Selektion ausschließen, die Population in bezug auf diesen einen Genlocus bei Panmixie eindeutig durch die Angabe p = 0,4 und q = 0,6 beschreiben.

Nach der Definition müssen alle Individuen einer lokalen Population nun gleiche Wahrscheinlichkeit haben, miteinander Nachkommen zu produzieren. Wir können daher die genetische Zusammensetzung der Nachkommen-Generation nach den Gesetzen der Wahrscheinlichkeit berechnen.

Es gilt allgemein. Die Wahrscheinlichkeit, dass zwei voneinander unabhängige Ereignisse zugleich auftreten, ist gleich dem Produkt der Einzelwahrscheinlichkeiten. Es ist also z. B. die Wahrscheinlichkeit, dass bei einem Würfel eine Eins geworfen wird, gleich 1/6. Die Wahrscheinlichkeit, dass bei gleichzeitigem Werfen von 2 Würfeln sowohl der eine als auch der andere eine 1 zeigt, ist gleich dem Produkt der Einzelwahrscheinlichkeiten.

Dies ergibt: 1/6 * 1/6 = 1/36.

Das Hardy-Weinberg-Gesetz ist leicht definierbar, wenn man vom Genpool ausgeht.

In diesem hat das Allel S die Häufigkeit p und s die Häufigkeit q. In der nächsten Generation werden die Allele zufällig zu Zweiergruppen kombiniert, wie es bei der Verschmelzung der Gameten ja tatsächlich der Fall ist.

Wir erhalten die Kombinationen SS, Ss und ss mit der Häufigkeitsverteilung

p² : 2pq : q².

Dieses Ergebnis entspricht dem Hardy-Weinberg - Gesetz.

Mit Hilfe dieser Überlegung können wir nach das Gesetz über den genetischen Aufbau einer Mendel - Population ableiten. Dazu können wir sowohl von den Individuen der Population selbst ausgehen, als auch vom Genpool. Im ersten Fall müssen wir uns zunächst fragen, wie viel verschiedene mögliche Paarungen es gibt und wie häufig jeder der einzelnen Paarungstypen zu erwarten ist. Da es sich um Zufallspaarung handelt, ist die Wahrscheinlichkeit, dass gerade etwa zwei schwarze Individuen zusammenkommen, gleich dem Produkt aus den Einzelhäufigkeiten. Wenn P die relative Häufigkeit der schwarzen, H die der grauen und Q die der weißen Individuen ist, dann erwarten wir also die Kreuzung Schwarz x Schwarz mit der Häufigkeit P X P =P² und Grau x Weiß mit der Häufigkeit H x Q + Q x H usw. Nachdem wir so die Erwartungshäufigkeit für die verschiedenen Paarungen ermittelt haben, müssen wir uns noch überlegen, welche Nachkommen jeweils aus den Kreuzungen zu erwarten sind.

Unter Berücksichtigung der Mendelschen Regeln können wir das leicht tun. Addieren wir nun die Erwartungshäufigkeiten der drei möglichen Farbtypen schwarz, grau oder weiß unter den Nachkommen, so erhalten wir die theoretische Verteilung.

Es ergibt sich, dass Schwarz, Grau und Weiß in der Nachkommenschaft so verteilt sein wird wie

(P+ 0,5 H)² : 2(P+0,5 H)(Q + 0,5 H)(Q + 0,5H)²

Viel leichter kommen wir zu einem Ergebnis, wenn wir vom Genpool ausgehen. In diesem hat das Allel S die Häufigkeit p und s die Häufigkeit q. In der nächsten Generation werden die Allele zufällig zu Zweiergruppen kombiniert, wie es bei der Verschmelzung der Gameten ja tatsächlich der Fall ist.

Wir erhalten die Kombinationen SS, Ss und ss mit der Häufigkeitsverteilung p2 : 2pq : q2.

Die Häufigkeit von S und s sind damit konstant geblieben. Solange jeder der drei in der Population koexistierenden Genotypen gleiche Überlebenschancen, gleiche Paarungschancen und gleiche Fruchtbarkeit (bzw. gleiche Fitness) besitzt und auch kein anderer populationsdynamischer Faktor wirksam ist, wird sich auch im Laufe weiterer Generationen nichts an der genetischen Zusammensetzung der Population ändern.

Die Hardy - Weinberg - Verteilung gibt uns also die stabile Gleichgewichtssituation in einer Population an, in der keine selektiven noch andere Kräfte wirksam sind. Wenn wir in Populationen eine Abweichung von dieser Verteilung feststellen können, müssen wir daher annehmen, dass diese durch eine unterschiedliche Überlebenswahrscheinlichkeit der verschiedenen Genotypen zustande gekommen ist oder die Paarung nicht rein zufällig erfolgt oder auch andere Kräfte wirksam sind.

Bei vielen populationsgenetischen Untersuchungen findet die theoretische Verteilung nach Hardy - Weinberg Anwendung. Da uns dadurch ein besserer Einblick über den Aufbau natürlicher Populationen gewährt wird, wollen auch wir einige Betrachtungen anstellen.

Zunächst wollen wir untersuchen, ob die Bedingungen der theoretisch sehr deutlich, dass bei intermediärem Erbgang die Population bei derselben genetischen Zusammensetzung dem Betrachter sehr mannigfaltig erscheint, während bei dominantem Erbgang eine einheitlich aufgebaute Population vorliegt, in der nur einige wenige, aberrante Typen vorkommen. Besonders dann, wenn von zwei oder mehreren Allelen das oder die rezessiven seltener sind, wird ein beachtlicher Teil der genetischen Variabilität im versteckten Zustand vorliegen und ohne genaue genetische Analyse dem Betrachter entgehen.

Nun sind aber Dominanz - Rezessiv - Verhältnisse bei vielen Merkmalen wesentlich häufiger als intermediäre Erbgänge, so dass wir mit diesem Phänomen häufig zu rechnen haben werden. So z.B. fanden Dubinin und Mitarbeiter in einer Wildpopulation der Taufliege Drosophila melanogaster unter 10.000 Individuen 37 mit schmalen Augen, 41 mit rauen Augen, 16 mit dunklen Augen, 2 mit "sepia" - Augen u. s. f. Greifen wir das seltenste heraus, nämlich "sepia". Dieses Merkmal ist aus Kreuzungsversuchen gut bekannt. Es beruht auf einem rezessiven Allel "se". Wir müssen also zunächst annehmen, dass se in natürlichen Populationen überhaupt keine Rolle spielt, da nur 2 unter 10000 Individuen das Merkmal "sepia" gezeigt haben. Da sie rezessiv gegenüber seinem Normalallel ist; das wir mit + bezeichnen wollen, müssen die beiden gefundenen Individuen homozygot se/se gewesen sein. Wenn wir annehmen, dass sich die Wildpopulation im Zufallsgleichgewicht befindet, kann mit Hilfe der Hardy - Weinberg - Verteilung die Häufigkeit von se in der Population leicht berechnet werden.

Zunächst wissen wir, dass die Verteilung +/+ : +/se : se/se gleich p2 :2pq: q2 sein muss.
Folglich ist in unserem Fall q2 =0,0002 und q = 0,0141. D. h., dass die Frequenz von se in der Population 1,41% beträgt. Noch weit unerwarteter ist die Heterozygotenhäufigkeit, die sich aus 2pq ergibt.
Da p+q=1 ist, schreiben wir 2pq=2q(1 - q) und erhalten in unserem Fall: Heterozygotenhäufigkeit = 2 * 0,0141 * 0,9859 = 0,0278. Etwa 3 % der Individuen der Population besitzen se also in heterozygotem Zustand. Wenn wir anfänglich behauptet haben, dass 'se'im Genpool der natürlichen Population keine Rolle spielt, da nur 2 unter 10000 Individuen das Merkmal gezeigt haben, so müssen wir nun doch erkennen, dass se immerhin ein Allel ist, das wir berücksichtigen müssen.

Die Erkenntnis, dass bei Rezessivität auch seltene Merkmale einer Population im Genpool eine Rolle spielen können, hat für mehrere, verschiedene Probleme Bedeutung. Es erscheint uns zunächst nun die Feststellung, dass eine bestimmte Population keine auffällige Variabilität hat in bezug auf morphologische, physiologische oder andere Eigenschaften, die mit der Lebenstüchtigkeit zu tun haben, als wenig beweisend. Erst wenn Methoden angewendet werden, die es erlauben, auch die versteckte genetische Variabilität aufzudecken, können wir eine befriedigende Beschreibung des Genpools erreichen. Bei der Besprechung der genetischen Bürde, werden wir auf dieses Problem zurückkommen.

Ein abschließendes Beispiel soll die Bedeutung der Hardy-Weinberg Verteilung bei menschlichen rezessiven Erbleiden verdeutlichen.

Eine rezessive Erbkrankheit sei in der Bevölkerung mit einer Häufigkeit von 1: 20.000 vertreten. Diese Krankheit kann als sehr selten bezeichnet werden. Nach Hardy Weinberg gilt

q² [aa] = 1/20000 = 0,00005

Daraus lässt sich q [Häufigkeit von a im Genpool] berechnen: q [a] = 0,00707

Da weiters gilt: p=1-q ist p [Häufigkeit von A] = 0,99293

Daraus errechnet sich schließlich die Heterozygotenhäufigkeit:

2pq [Aa] = 0,014 (1,4%)

Wir stellen fest: Wenn in einer Population eine Erbkrankheit zu 0,005% (jeder Zweihundertste) auftritt, dann sind etwa 1,4% (jeder Siebzigste) der Menschen Überträger für eben diese Krankheit.
(Siehe dazu auch das Arbeitsblatt).